# 第10章 二叉搜索树
# 10.1 二叉搜索树
# 概念
二叉搜索树（BST）是二叉树的一种，但是只允许你在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大的值。
# 树的实现
中序遍历是一种以上行顺序访问 BST 所有节点的遍历方式，也就是说以从最小到最大的顺序访问所有节点。中序遍历的一种应用就是对树进行排序操作。
先序遍历是以优先于后代节点的顺序访问每个节点。
后序遍历是先访问节点的后代节点，再访问节点本身。后序遍历的一种应用是计算一个目录及子目录中所有文件所占空间的大小。
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1,
EQUALS: 0
}
function defaultCompare(a, b) {
if (a === b) {
return Compare.EQUALS
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN
}
class Node {
constructor(key) {
this.key = key
this.left = undefined
this.right = undefined
}
toString() {
return `${this.key}`
}
}
class BinarySearchTree {
constructor(compareFn = defaultCompare) {
this.compareFn = compareFn
this.root = undefined
}
insert(key) {
// special case: first key
if (this.root == null) {
this.root = new Node(key)
} else {
this.insertNode(this.root, key)
}
}
insertNode(node, key) {
if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
if (node.left == null) {
node.left = new Node(key)
} else {
this.insertNode(node.left, key)
}
} else if (node.right == null) {
node.right = new Node(key)
} else {
this.insertNode(node.right, key)
}
}
getRoot() {
return this.root
}
//搜索一个特定值
search(key) {
return this.searchNode(this.root, key)
}
searchNode(node, key) {
if (node == null) {
return false
}
if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
return this.searchNode(node.left, key)
}
if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
return this.searchNode(node.right, key)
}
return true
}
inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root, callback)
}
inOrderTraverseNode(node, callback) {
if (node != null) {
this.inOrderTraverseNode(node.left, callback)
callback(node.key)
this.inOrderTraverseNode(node.right, callback)
}
}
preOrderTraverse(callback) {
this.preOrderTraverseNode(this.root, callback)
}
preOrderTraverseNode(node, callback) {
if (node != null) {
callback(node.key)
this.preOrderTraverseNode(node.left, callback)
this.preOrderTraverseNode(node.right, callback)
}
}
postOrderTraverse(callback) {
this.postOrderTraverseNode(this.root, callback)
}
postOrderTraverseNode(node, callback) {
if (node != null) {
this.postOrderTraverseNode(node.left, callback)
this.postOrderTraverseNode(node.right, callback)
callback(node.key)
}
}
//搜索最小的值
min() {
return this.minNode(this.root)
}
minNode(node) {
let current = node
while (current != null && current.left != null) {
current = current.left
}
return current
}
//搜索最大值
max() {
return this.maxNode(this.root)
}
maxNode(node) {
let current = node
while (current != null && current.right != null) {
current = current.right
}
return current
}
remove(key) {
this.root = this.removeNode(this.root, key)
}
removeNode(node, key) {
if (node == null) {
return undefined
}
if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
node.left = this.removeNode(node.left, key)
return node
}
if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
node.right = this.removeNode(node.right, key)
return node
}
// key is equal to node.item
// handle 3 special conditions
// 1 - a leaf node
// 2 - a node with only 1 child
// 3 - a node with 2 children
// case 1
if (node.left == null && node.right == null) {
node = undefined
return node
}
// case 2
if (node.left == null) {
node = node.right
return node
}
if (node.right == null) {
node = node.left
return node
}
// case 3 //重构一个二叉搜索树
const aux = this.minNode(node.right)
node.key = aux.key
node.right = this.removeNode(node.right, aux.key)
return node
}
}
const tree = new BinarySearchTree()
tree.insert(1)
tree.insert(3)
tree.insert(8)
tree.insert(10)
tree.insert(14)
tree.insert(13)
tree.insert(4)
tree.insert(6)
tree.insert(7)
document.write(`<br>中序遍历`)
tree.inOrderTraverse(v => document.write(`${v}\n`)) //中序遍历1 3 4 6 7 8 10 13 14
document.write("<br>前序遍历")
tree.preOrderTraverse(v => document.write(`${v}\n`)) //前序遍历1 3 8 4 6 7 10 14 13
document.write("<br>后序遍历")
tree.postOrderTraverse(v => document.write(`${v}\n`)) //后序遍历7 6 4 13 14 10 8 3 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
# 10.2 自平衡树
# 概念
AVL(Adelson-Velskii-Landi)树是一种自平衡二叉搜索树，意思是任何一个节点左右两侧子树的高度之差最多为1.
# 实现
在AVL树中，需要对每个节点计算右子树和左子树之间的差值，该值应为0、1、-1.如果结果不是这三个值之一，则需要平衡该AVL树。
向AVL树插入节点时，可以执行单旋转或双旋转两种平衡操作，分别对应四种场景： 左-左（LL）:向右的单旋转。:这种情况出现于节点的左侧子节点的高度大于右侧子节点的高度时，并且左侧子节点也是平衡或左侧较重的。
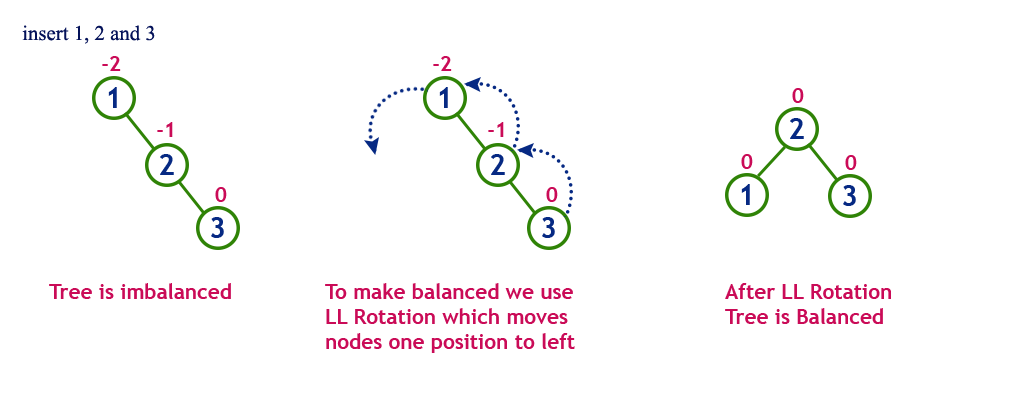
右-右（RR）:向左的单旋转。:这种情况出现于节点的右侧子节点的高度大于左侧子节点的高度时，并且右侧子节点也是平衡或右侧较重的。
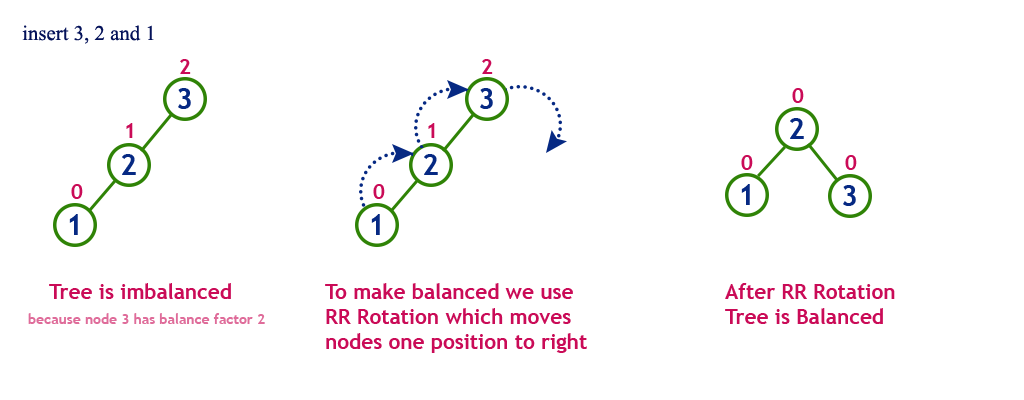
左-右（LR）:先左旋再右旋。先RR再LL。:这种情况出现于左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重的。
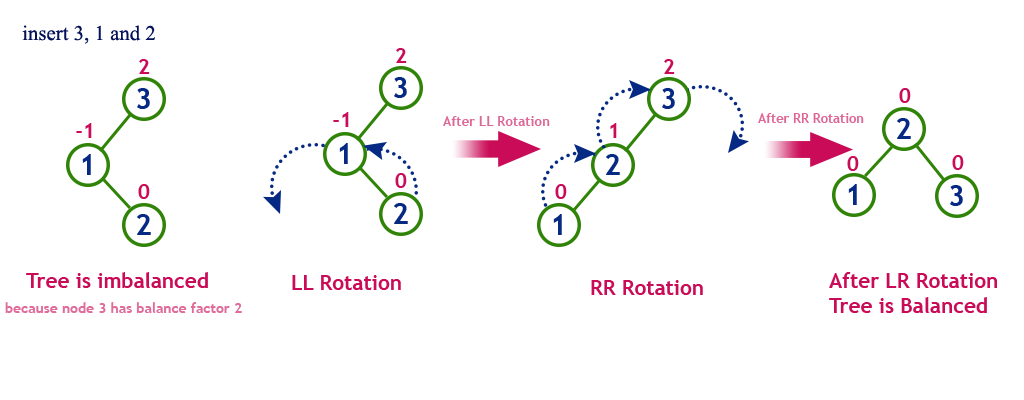
右-右（RL）:先右旋再左旋。先LL再RR。:这种情况出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重的。
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1,
EQUALS: 0
};
function defaultCompare(a, b) {
if (a === b) {
return Compare.EQUALS;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
class Node {
constructor(key) {
this.key = key;
this.left = undefined;
this.right = undefined;
}
toString() {
return `${this.key}`;
}
}
class AVLTree extends BinarySearchTree {
constructor(compareFn = defaultCompare) {
super(compareFn);
this.compareFn = compareFn;
this.root = null;
}
getNodeHeight(node) {
if (node == null) {
return -1;
}
return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}
/**
* Left left case: rotate right
*
* b a
* / \ / \
* a e -> rotationLL(b) -> c b
* / \ / \
* c d d e
*
* @param node Node<T>
*/
rotationLL(node) {
const tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}
/**
* Right right case: rotate left
*
* a b
* / \ / \
* c b -> rotationRR(a) -> a e
* / \ / \
* d e c d
*
* @param node Node<T>
*/
rotationRR(node) {
const tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}
/**
* Left right case: rotate left then right
* @param node Node<T>
*/
rotationLR(node) {
node.left = this.rotationRR(node.left);
return this.rotationLL(node);
}
/**
* Right left case: rotate right then left
* @param node Node<T>
*/
rotationRL(node) {
node.right = this.rotationLL(node.right);
return this.rotationRR(node);
}
getBalanceFactor(node) {
const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
switch (heightDifference) {
case -2:
return BalanceFactor.UNBALANCED_RIGHT;
case -1:
return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
case 1:
return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
case 2:
return BalanceFactor.UNBALANCED_LEFT;
default:
return BalanceFactor.BALANCED;
}
}
insert(key) {
this.root = this.insertNode(this.root, key);
}
insertNode(node, key) {
if (node == null) {
return new Node(key);
} if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
node.left = this.insertNode(node.left, key);
} else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
node.right = this.insertNode(node.right, key);
} else {
return node; // duplicated key
}
// verify if tree is balanced
const balanceFactor = this.getBalanceFactor(node);
if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) {
// Left left case
node = this.rotationLL(node);
} else {
// Left right case
return this.rotationLR(node);
}
}
if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) {
// Right right case
node = this.rotationRR(node);
} else {
// Right left case
return this.rotationRL(node);
}
}
return node;
}
removeNode(node, key) {
node = super.removeNode(node, key); // {1}
if (node == null) {
return node;
}
// verify if tree is balanced
const balanceFactor = this.getBalanceFactor(node);
if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
// Left left case
if (
this.getBalanceFactor(node.left) === BalanceFactor.BALANCED
|| this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
) {
return this.rotationLL(node);
}
// Left right case
if (this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {
return this.rotationLR(node.left);
}
}
if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
// Right right case
if (
this.getBalanceFactor(node.right) === BalanceFactor.BALANCED
|| this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
) {
return this.rotationRR(node);
}
// Right left case
if (this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {
return this.rotationRL(node.right);
}
}
return node;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
# 10.3 红黑树
# 概念
红黑树也是一个自平衡二叉搜索树。AVL树插入和移除节点可能会造成旋转，所以我们需要一个包含多次插入和删除的自平衡树，红黑树是比较好的。如果插入和删除的频率较低，那么AVL树比红黑树更好。
在红黑树中，每个节点都遵循以下规则：
- 每个节点不是红的就是黑的
- 树的根节点是黑的
- 所有叶节点都是黑的
- 如果一个节点是红的，那么它的两个子节点都是黑的
- 不能有两个相邻的红结点，一个红节点不能有红的父节点或子节点
- 从给定的节点到它的后代节点的所有路径中包含相同数量的黑色节点
# 实现
有以下场景：
- uncle节点时红色的。
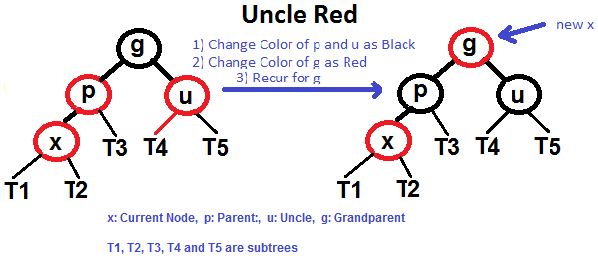
- uncle节点是黑色的： 2.1 左—左（LL）:父节点是祖父节点的左侧子节点，节点是父节点的左侧子节点。
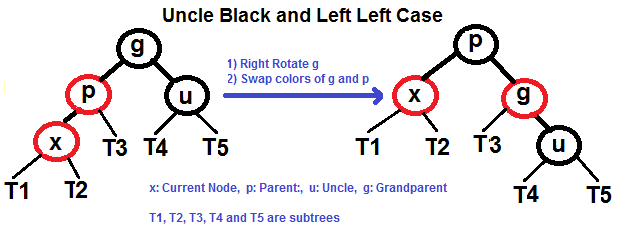
2.2 左—右（LR）:父节点是祖父节点的左侧子节点，节点是父节点的右侧子节点。
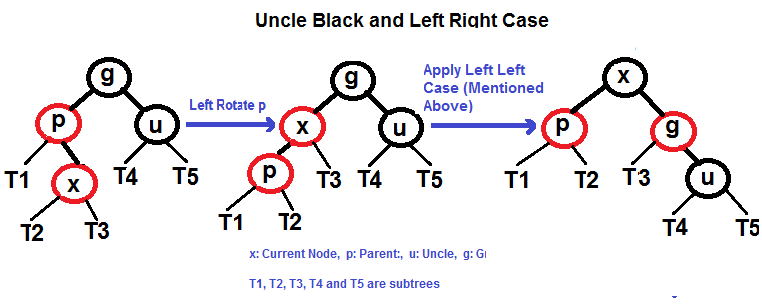
2.3 右—右（RR）:父节点是祖父节点的右侧子节点，节点是父节点的右侧子节点。
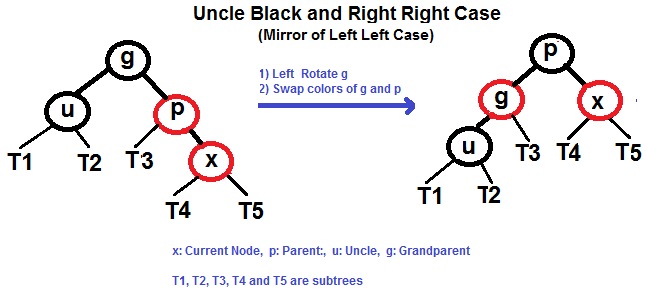
2.4 左—左（RL）:父节点是祖父节点的右侧子节点，节点是父节点的左侧子节点。
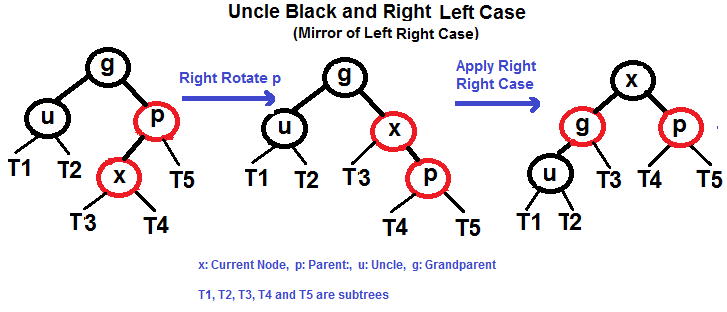
// Possible colors of red-black tree nodes.
const RED_BLACK_TREE_COLORS = {
red: 'red',
black: 'black',
};
// Color property name in meta information of the nodes.
const COLOR_PROP_NAME = 'color';
export default class RedBlackTree extends BinarySearchTree {
/**
* @param {*} value
* @return {BinarySearchTreeNode}
*/
insert(value) {
const insertedNode = super.insert(value);
// if (!this.root.left && !this.root.right) {
if (this.nodeComparator.equal(insertedNode, this.root)) {
// Make root to always be black.
this.makeNodeBlack(insertedNode);
} else {
// Make all newly inserted nodes to be red.
this.makeNodeRed(insertedNode);
}
// Check all conditions and balance the node.
this.balance(insertedNode);
return insertedNode;
}
/**
* @param {*} value
* @return {boolean}
*/
remove(value) {
throw new Error(`Can't remove ${value}. Remove method is not implemented yet`);
}
/**
* @param {BinarySearchTreeNode} node
*/
balance(node) {
// If it is a root node then nothing to balance here.
if (this.nodeComparator.equal(node, this.root)) {
return;
}
// If the parent is black then done. Nothing to balance here.
if (this.isNodeBlack(node.parent)) {
return;
}
const grandParent = node.parent.parent;
if (node.uncle && this.isNodeRed(node.uncle)) {
// If node has red uncle then we need to do RECOLORING.
// Recolor parent and uncle to black.
this.makeNodeBlack(node.uncle);
this.makeNodeBlack(node.parent);
if (!this.nodeComparator.equal(grandParent, this.root)) {
// Recolor grand-parent to red if it is not root.
this.makeNodeRed(grandParent);
} else {
// If grand-parent is black root don't do anything.
// Since root already has two black sibling that we've just recolored.
return;
}
// Now do further checking for recolored grand-parent.
this.balance(grandParent);
} else if (!node.uncle || this.isNodeBlack(node.uncle)) {
// If node uncle is black or absent then we need to do ROTATIONS.
if (grandParent) {
// Grand parent that we will receive after rotations.
let newGrandParent;
if (this.nodeComparator.equal(grandParent.left, node.parent)) {
// Left case.
if (this.nodeComparator.equal(node.parent.left, node)) {
// Left-left case.
newGrandParent = this.leftLeftRotation(grandParent);
} else {
// Left-right case.
newGrandParent = this.leftRightRotation(grandParent);
}
} else {
// Right case.
if (this.nodeComparator.equal(node.parent.right, node)) {
// Right-right case.
newGrandParent = this.rightRightRotation(grandParent);
} else {
// Right-left case.
newGrandParent = this.rightLeftRotation(grandParent);
}
}
// Set newGrandParent as a root if it doesn't have parent.
if (newGrandParent && newGrandParent.parent === null) {
this.root = newGrandParent;
// Recolor root into black.
this.makeNodeBlack(this.root);
}
// Check if new grand parent don't violate red-black-tree rules.
this.balance(newGrandParent);
}
}
}
/**
* Left Left Case (p is left child of g and x is left child of p)
* @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
* @return {BinarySearchTreeNode}
*/
leftLeftRotation(grandParentNode) {
// Memorize the parent of grand-parent node.
const grandGrandParent = grandParentNode.parent;
// Check what type of sibling is our grandParentNode is (left or right).
let grandParentNodeIsLeft;
if (grandGrandParent) {
grandParentNodeIsLeft = this.nodeComparator.equal(grandGrandParent.left, grandParentNode);
}
// Memorize grandParentNode's left node.
const parentNode = grandParentNode.left;
// Memorize parent's right node since we're going to transfer it to
// grand parent's left subtree.
const parentRightNode = parentNode.right;
// Make grandParentNode to be right child of parentNode.
parentNode.setRight(grandParentNode);
// Move child's right subtree to grandParentNode's left subtree.
grandParentNode.setLeft(parentRightNode);
// Put parentNode node in place of grandParentNode.
if (grandGrandParent) {
if (grandParentNodeIsLeft) {
grandGrandParent.setLeft(parentNode);
} else {
grandGrandParent.setRight(parentNode);
}
} else {
// Make parent node a root
parentNode.parent = null;
}
// Swap colors of granParent and parent nodes.
this.swapNodeColors(parentNode, grandParentNode);
// Return new root node.
return parentNode;
}
/**
* Left Right Case (p is left child of g and x is right child of p)
* @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
* @return {BinarySearchTreeNode}
*/
leftRightRotation(grandParentNode) {
// Memorize left and left-right nodes.
const parentNode = grandParentNode.left;
const childNode = parentNode.right;
// We need to memorize child left node to prevent losing
// left child subtree. Later it will be re-assigned to
// parent's right sub-tree.
const childLeftNode = childNode.left;
// Make parentNode to be a left child of childNode node.
childNode.setLeft(parentNode);
// Move child's left subtree to parent's right subtree.
parentNode.setRight(childLeftNode);
// Put left-right node in place of left node.
grandParentNode.setLeft(childNode);
// Now we're ready to do left-left rotation.
return this.leftLeftRotation(grandParentNode);
}
/**
* Right Right Case (p is right child of g and x is right child of p)
* @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
* @return {BinarySearchTreeNode}
*/
rightRightRotation(grandParentNode) {
// Memorize the parent of grand-parent node.
const grandGrandParent = grandParentNode.parent;
// Check what type of sibling is our grandParentNode is (left or right).
let grandParentNodeIsLeft;
if (grandGrandParent) {
grandParentNodeIsLeft = this.nodeComparator.equal(grandGrandParent.left, grandParentNode);
}
// Memorize grandParentNode's right node.
const parentNode = grandParentNode.right;
// Memorize parent's left node since we're going to transfer it to
// grand parent's right subtree.
const parentLeftNode = parentNode.left;
// Make grandParentNode to be left child of parentNode.
parentNode.setLeft(grandParentNode);
// Transfer all left nodes from parent to right sub-tree of grandparent.
grandParentNode.setRight(parentLeftNode);
// Put parentNode node in place of grandParentNode.
if (grandGrandParent) {
if (grandParentNodeIsLeft) {
grandGrandParent.setLeft(parentNode);
} else {
grandGrandParent.setRight(parentNode);
}
} else {
// Make parent node a root.
parentNode.parent = null;
}
// Swap colors of granParent and parent nodes.
this.swapNodeColors(parentNode, grandParentNode);
// Return new root node.
return parentNode;
}
/**
* Right Left Case (p is right child of g and x is left child of p)
* @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
* @return {BinarySearchTreeNode}
*/
rightLeftRotation(grandParentNode) {
// Memorize right and right-left nodes.
const parentNode = grandParentNode.right;
const childNode = parentNode.left;
// We need to memorize child right node to prevent losing
// right child subtree. Later it will be re-assigned to
// parent's left sub-tree.
const childRightNode = childNode.right;
// Make parentNode to be a right child of childNode.
childNode.setRight(parentNode);
// Move child's right subtree to parent's left subtree.
parentNode.setLeft(childRightNode);
// Put childNode node in place of parentNode.
grandParentNode.setRight(childNode);
// Now we're ready to do right-right rotation.
return this.rightRightRotation(grandParentNode);
}
/**
* @param {BinarySearchTreeNode|BinaryTreeNode} node
* @return {BinarySearchTreeNode}
*/
makeNodeRed(node) {
node.meta.set(COLOR_PROP_NAME, RED_BLACK_TREE_COLORS.red);
return node;
}
/**
* @param {BinarySearchTreeNode|BinaryTreeNode} node
* @return {BinarySearchTreeNode}
*/
makeNodeBlack(node) {
node.meta.set(COLOR_PROP_NAME, RED_BLACK_TREE_COLORS.black);
return node;
}
/**
* @param {BinarySearchTreeNode|BinaryTreeNode} node
* @return {boolean}
*/
isNodeRed(node) {
return node.meta.get(COLOR_PROP_NAME) === RED_BLACK_TREE_COLORS.red;
}
/**
* @param {BinarySearchTreeNode|BinaryTreeNode} node
* @return {boolean}
*/
isNodeBlack(node) {
return node.meta.get(COLOR_PROP_NAME) === RED_BLACK_TREE_COLORS.black;
}
/**
* @param {BinarySearchTreeNode|BinaryTreeNode} node
* @return {boolean}
*/
isNodeColored(node) {
return this.isNodeRed(node) || this.isNodeBlack(node);
}
/**
* @param {BinarySearchTreeNode|BinaryTreeNode} firstNode
* @param {BinarySearchTreeNode|BinaryTreeNode} secondNode
*/
swapNodeColors(firstNode, secondNode) {
const firstColor = firstNode.meta.get(COLOR_PROP_NAME);
const secondColor = secondNode.meta.get(COLOR_PROP_NAME);
firstNode.meta.set(COLOR_PROP_NAME, secondColor);
secondNode.meta.set(COLOR_PROP_NAME, firstColor);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
← 第9章 递归 第11章 二叉堆和堆排序 →